21.3. Handling Collisions¶
In practice, there will be many more possible keys than there are slots in the hash table. Think about our MHCHashMap implementation where there are only 100 slots by default, but there can be limitless possible keys (such as strings of any length). So, we need to handle the situation where two keys hash to the same slot. This is called a collision.
There are two common strategies for resolving collisions: linear probing and chaining.
Linear Probing: After finding a collision, we place the new key-value pair in the next available slot in the array.
Chaining: After finding a collision, we place the new key-value pair in a secondary List data structure stored at the slot in the array.
Here, we’ll focus on chaining as a collision resolution strategy.
21.3.1. Chaining¶
A straightforward way of implementing chaining is to define each slot in the hash table to be the beginning of a List. All records that hash to a particular slot are placed on that slot’s list. The following figure illustrates a hash table where each slot points to a linked list to hold the records associated with that slot. The hash function used in the example is just the key itself modulo the array capacity:
int getIndex(int key) {
return key % CAPACITY;
}
Note
In the diagram above, we only show the keys in the linked lists for simplicity. In our actual implementation, we will store KeyValuePair objects in the list entries as well. The capacity of the hash table is 10 so for example, the keys 100 and 930 both hash to slot 0:
100 % 10 = 0930 % 10 = 0
Thus these two keys will be stored in the linked list at slot 0.
Given a table of capacity \(M\) storing \(N\) records, the hash function will (ideally) spread the records evenly among the \(M\) positions in the table, yielding on average \(N/M\) records for each list. Assuming that the table has more slots than there are records to be stored, we can hope that few slots will contain more than one record. In the case where a list is empty or has only one record, a search requires only one access to the list. Thus, the average cost for hashing should be \(O(1)\). However, if a poor hash function causes many records to hash to only a few of the slots, then the cost to access a record will be much higher because many elements on the linked list must be searched.
21.3.2. MHCHashMap, with chaining¶
We modify our MHCHashMap implementation to use chaining, which we call MHCHashMapChaining:
public class MHCHashMapChaining<K, V> implements MHCMap<K, V> {
// Size of the table.
private static final int CAPACITY = 100;
// Holds the key-value pairs that have been inserted
private List<KeyValuePair<K,V>>[] entries;
The main difference is the type of our entries array. Instead of maintaining an array of KeyValuePair objects, we maintain an array of List objects. Each List object stores the KeyValuePair objects that hash to the same slot.
21.3.3. MHCHashMapChaining get()¶
We focus on how the get() method implementation differs from the MHCHashMap implementation:
/**
* Get the value associated with a key
* @param key the key to look up
* @return the value associated with the key or null if the key is not
* in the map.
*/
@Override
public V get(K key) {
KeyValuePair<K,V> pair = getPair(key);
if (pair == null) {
return null;
}
else {
return pair.getValue();
}
}
You’ll notice that the get() method calls a helper method getPair() to get the KeyValuePair object for the given key. Otherwise, it closely mirrors the implementation of get() in MHCHashMap.
We’ll look at the implementation of getPair() next.
/**
* Get the key-value pair for the given key
* @param key the key to search for
* @return the key-value pair with the right key,
* or null if the key is not in the table
*/
private KeyValuePair<K, V> getPair (K key) {
// Get the entry at the given index
int index = getIndex(key);
List<KeyValuePair<K,V>> entry = entries[index];
// There is no entry at this index
if (entry == null) {
return null;
}
// There is a list at the index. Search for
// the right key
for (int i = 0; i < entry.size(); i++) {
KeyValuePair<K,V> pair = entry.get(i);
if (pair.getKey().equals(key)) {
return pair;
}
}
// The key was not in the list
return null;
}
The getPair() method takes a key as input and returns the KeyValuePair object associated with that key. If the key is not found, it returns null. It begins by computing the index for the key using getIndex(), and then it retrieves the List object at that index.
If the List object is null, then the key is not in the map, so the method returns null.
Otherwise, the method iterates through the List to find the KeyValuePair with the matching key. If it finds a match, it returns the KeyValuePair object. If it doesn’t find a match, it returns null.
21.3.4. Hash Table Operation Analysis¶
How efficient is hashing? We can measure hashing performance in terms of the number of record accesses required when performing an operation.
When the hash table is empty, the first record inserted will always find its home position free. Thus, it will require only one record access to find a free slot. If all records are stored in their home positions, then successful searches will also require only one record access. As the table begins to fill up, the probability that a record can be inserted into its home position decreases. If a record hashes to an occupied slot, then the collision resolution policy must locate another slot in which to store it. Finding records not stored in their home position also requires additional record accesses as the record is searched for along its probe sequence. As the table fills up, more and more records are likely to be located ever further from their home positions.
From this discussion, we see that the expected cost of hashing is a function of how full the table is. We define the load factor of the table as \(N/M\), where \(N\) is the number of records currently in the table.
The load factor tells us about the tradeoff between the speed of operations and the memory usage of the hash table. A low load factor means that the hash table is not very full, so operations are fast but the memory usage is high as there are many empty slots in the table. A high load factor means that the hash table is very full, so operations are slow but the memory usage is low as there are fewer empty slots in the table. Below is a plot showing the theoretical growth rate of the cost for insertion and deletion into a hash table as the load factor increases. The horizontal axis is the value of the load factor, while the vertical axis is the expected number of accesses to the hash table. The solid lines show a theoretical lower bound on the cost, while the dashed lines show the upper bound on the cost, so the two lines together give us a range of expected costs for both inserting and deleting:
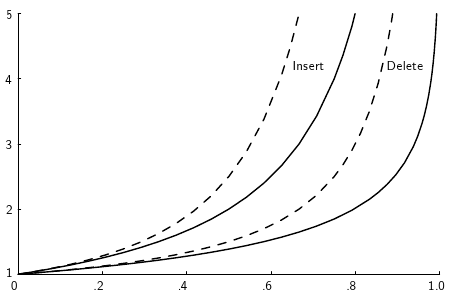
From the figure, we can see that the cost for hashing when the table is not too full is typically close to one record access. This is extraordinarily efficient, much better than binary search which requires \(O(\log n)\) record accesses. As the load factor increases, so does the expected cost. A typical rule of thumb is to keep the load factor around 0.75, which means that the hash table is about 75% full. This ensures that the hash table is not too full, so operations are fast, but also not too empty, so memory usage is low.
This requires that the implementor have some idea of how many records are likely to be in the table at maximum loading, and select the table size accordingly. The goal should be to make the table small enough so that it does not waste a lot of space on the one hand, while making it big enough to keep performance good on the other.
Below is a table comparing the time complexities of the operations for three data structures we’ve discussed: a sorted ArrayList, a balanced BST, and a hash table with a low load factor:
Operation |
Sorted ArrayList |
Balanced BST |
Hash Table w/ low load factor |
|---|---|---|---|
Get at position |
O(1) |
N/A |
N/A |
Can change size? |
Yes |
Yes |
Yes |
Insert |
O(n) |
O(log(n)) |
O(1) |
Remove |
O(n) |
O(log(n)) |
O(1) |
Find value |
O(log(n)) |
O(log(n)) |
O(1) |
Produce sorted order |
O(n) |
O(n) |
N/A |
Memory |
Often has unused entries |
Each node requires left & right fields |
.75 load => 1/4 empty, nodes in chain need next field |
21.3.5. MHCHashMapChaining Complete Reference¶
The complete implementation of MHCHashMapChaining can be found in the code block below as a reference:
/**
* A hash table implementation of a Map.
* K is the type of the keys used
* V is the type of the values associated with the keys.
*/
public class MHCHashMapChaining<K, V> implements MHCMap<K, V> {
// Size of the table.
private static final int CAPACITY = 100;
// Holds the key-value pairs that have been inserted
private List<KeyValuePair<K,V>>[] entries;
@SuppressWarnings("unchecked")
public MHCHashMapChaining() {
entries = new ArrayList[CAPACITY];
}
/**
* Get the value associated with a key
* @param key the key to look up
* @return the value associated with the key or null if the key is not
* in the map.
*/
@Override
public V get(K key) {
KeyValuePair<K,V> pair = getPair(key);
if (pair == null) {
return null;
}
else {
return pair.getValue();
}
}
/**
* Get the key-value pair for the given key
* @param key the key to search for
* @return the key-value pair with the right key,
* or null if the key is not in the table
*/
private KeyValuePair<K, V> getPair (K key) {
// Get the entry at the given index
int index = getIndex(key);
List<KeyValuePair<K,V>> entry = entries[index];
// There is no entry at this index
if (entry == null) {
return null;
}
// There is a list at the index. Search for
// the right key
for (int i = 0; i < entry.size(); i++) {
KeyValuePair<K,V> pair = entry.get(i);
if (pair.getKey().equals(key)) {
return pair;
}
}
// The key was not in the list
return null;
}
/**
* Find the index into the array for the given key
* @param key the key being looked up
* @return the position in the table for the key
*/
private int getIndex(K key) {
// Get the hash code for the key.
int hashValue = key.hashCode();
// Mod the hashvalue by the capacity of the array to
// get a valid index
int index = Math.abs(hashValue) % CAPACITY;
System.out.println (key + " hashes to " + hashValue);
System.out.println ("index is " + index);
return index;
}
/**
* Associates a value with a key.
* @param key the key whose value is set
* @param value the value to be associated with the key
* @return if the key previously had a value, return the previous value. If the key
* was not in the table, return null.
*/
@Override
public V put(K key, V value) {
KeyValuePair<K, V> pair = getPair(key);
if (pair == null) {
int index = getIndex(key);
List<KeyValuePair<K, V>> entry = entries[index];
// No entry at that index currently
if (entry == null) {
entry = new ArrayList<>();
entry.add(new KeyValuePair<>(key, value));
entries[index] = entry;
return null;
}
// Entry already exists at that index. Add to the end of the list.
else {
entry.add(new KeyValuePair<>(key, value));
return null;
}
}
else {
V oldValue = pair.putValue(value);
return oldValue;
}
}
/**
* Returns true if the map has an entry for the key
* @param key the key to look up
* @return true if the key is in the table. Otherwise return false.
*/
@Override
public boolean containsKey(K key) {
return getPair(key) != null;
}
/**
* Removes the entry for the key.
* @param key the key for the entry to remove
* @return If the key was in the table, the value previously associated with
* the key is returned. If the key was not in the table, null is returned.
*/
@Override
public V remove(K key) {
int index = getIndex(key);
List<KeyValuePair<K, V>> entry = entries[index];
// No entry at that index; just return
if (entry == null) {
return null;
}
// Entry exists. Search for the right key
for (int i = 0; i < entry.size(); i++) {
KeyValuePair<K, V> pair = entry.get(i);
if (pair.getKey().equals(key)) {
//Save the value currently stored
// so it can be returned
V oldValue = pair.getValue();
entry.remove(i);
return oldValue;
}
}
// Key not found
return null;
}
}

